
自分自身も高校受験や大学受験の時、気にしてはいたんだけど。
でも、わかると便利な数字なんですよ!
あそこの学校は偏差値いくつ、といった言い方をよく耳にしますよね。
子供が中学受験のために模擬試験を受けて、久しぶりに偏差値に出会った方もいるのでは。
受験のたびにおつき合いすることになるものの、なんだかよくわからない・・・。
今回は、そんな「偏差値」について、
- どんなもの?
- 算出の仕方
- 偏差値を出すメリット・デメリット
- 高い低いの基準
- 高い偏差値をとるにはどうしたらいい?
といったことを、子供にもわかりやすく解説していきます。
目次
偏差値とは?
どうやって計算して出すの?
受験シーズンになるとよく耳にする「偏差値」。
偏差値は、集団の中での位置を知るための指標です。
テストが返された時、まず目に飛び込むのは点数ですよね。
でも、「やった、90点だ!」と思ったらまわりに100点の子がいっぱいで、平均点以下・・・なんてことも。
かと思えば、同じ90点でも、みんなが50点くらいだったら「成績優秀!」ということになりますよね。
成績を知るには、点数そのものでなく、集団の中での位置を知ることが大切なのです。
国語と算数のテストの結果です。
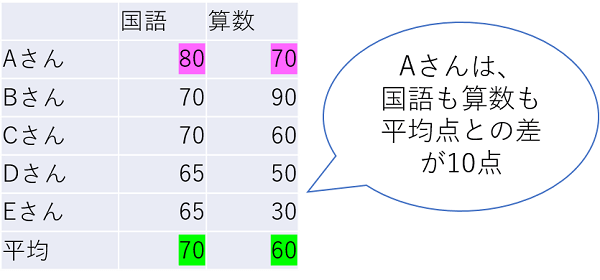
Aさんは、国語も算数も平均点との差は10点です。
ところが、国語は先生にほめられましたが、算数は特別よい成績とは評価されませんでした。

このように、平均点との差だけでは、集団の中の位置を正しく把握することができないのです。
よく見ると、国語はほかの人の点が平均点近くに集中していて、算数はバラバラなのがわかりますね。
このように、テストによってばらつきが異なると、自分の位置が変わってくるのです。
偏差値で見ると、ばらつきの少ない国語での高得点をとった国語の偏差値は68.3と高い数値になります。
これに対し、ばらつきの大きい算数の偏差値は55.0と国語に比べてかなり低くなるのです。
算出方法
偏差値の計算式は・・・

「標準偏差(ばらつきの程度)」というのは、受験者一人一人の点数が平均点を中心にどれだけばらついているかということです。
標準偏差の計算式は、以下のようになります。

考え方だけわかっていれば十分です。
実際のところ、受験者一人ひとりの点数なんて知るよしもないので、この計算式を覚えていても使う機会はまずないでしょう。
なので、受験生あるいはママとしては、考え方を知っていれば十分です。
要するに、
- その集団の個々の点数が平均を中心にどれだけばらついているかに注目
- 偏差値はそのばらつきの中での(自分の)位置を示す指標
ということです。
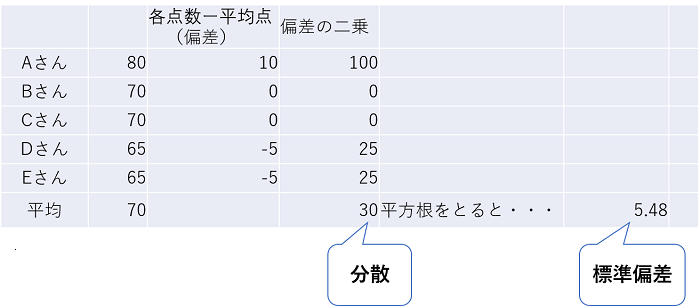
まず、標準偏差を求めます。
順を追って出していきましょう。
- 平均値を求める
- 「各点数ー平均点」(偏差)を全部出す
- 上記b(偏差)をそれぞれ二乗する
- 上記cの平均を求める(「分散」といいます)
- 上記d(分散)の平方根を求める(標準偏差)
先ほどの国語の場合、下のようになります。
Aさんの偏差値は、最初の式にあてはめて、
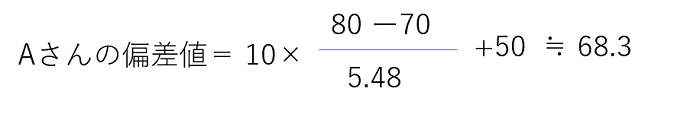
となります。
偏差値を出すメリット・デメリットは?
偏差値のメリットは
- レベルの違うテストの比較ができること
- ばらつきの違うテストの比較ができること
という2つ。
【メリット1】レベルの違うテストの比較ができること
偏差値は、難しい(平均点が低い)テストでも簡単な(平均点が高い)テストでも、平均点をとった場合は50になるように計算されます。
テストは、教科によって、あるいは同じ教科でも毎回平均点は違うものですよね。
なので、単純にとった点数で比べることはできませんが、基準が50に設定されている偏差値なら、
- 違う教科と比べる
- 前回のテストと比べる
といったことが可能なのです。

【メリット2】ばらつきの違うテストの比較ができること
先ほどの例に戻ると・・・

Aさんの集団内で位置がばらつきの違う2つのテストで変わってくることはなんとなくわかりますが、はっきりしません。
偏差値を出すと、
- 国語は68.3
- 算数は55.0
とずいぶん違うことがわかります。
デメリットはあるの?
偏差値は、テストを受けた集団の中での位置を示す数字です。
優秀なグループの平均点でも50だし、勉強の苦手なグループの平均点でも50です。
なので、たとえば模擬試験を受けて偏差値が高く出ても、受験しようと思っている学校の受験者のレベルが模擬試験を受けた集団よりずっと高かったりしたら手放しでは喜べません。
繰り返しますが、あくまでも集団の中での位置だということに注意しましょう。
偏差値の高い・低いの基準は?
偏差値は、下の式で算出します。

平均点をとると、「Aさんの点数ー平均点」の部分が0になり、偏差値が50になるのがわかりますよね?
このように、偏差値は、平均点をとった時に50になるよう設定されているのです。
また、
- 平均点より高ければ、「Aさんの点数ー平均点」の部分がプラスになるので、50より大きくなる
- 平均点より低ければ、「Aさんの点数ー平均点」の部分がマイナスになるので、50より小さくなる
となります。
つまり、50が平均で、それより高ければ優秀、低ければ低い程、学力的に劣るという判断になるというわけです。
高い偏差値をとるにはどうしたらいいの?
偏差値を求める計算式の中の

の部分を大きくしたいのですから、分母(標準偏差)を小さく、分子(Aさんの点数ー平均点)を大きくすればよいですね。
なので、
- 標準偏差の小さい(=平均点付近にみんなが集中している)テストで
- 平均点よりずっと高い点をとる。(=平均点が低い時に高得点をとる)
ということになります。
つまり、「みんな点をとれないテストで一人だけ高得点をとる」ことができればOKです。
といってもなかなか難しそうですが・・・

また、いうまでもありませんが、そうやって偏差値を上げたからといって希望の学校に合格できるというわけではありません。
偏差値を上げることにばかりエネルギーを使わないように気をつけましょう。
最後に
今回のまとめです。
- 偏差値は集団の中での位置を知るための指標
- 平均点が違うテスト、点数のばらつきの違うテストでも比較できる
- あくまでも1つの集団の中での位置を示す指標であることに注意
- 平均点をとった時に50になるようなっている
- みんなが低い点数の時に一人だけ高得点だと高い偏差値が出る
いかがでしたか?
ちょっとややこしいですが、偏差値の意味を理解して、上手につきあっていけるといいですね。






